수체계

셈, 비교, 계산, 순서결정, 측량, 값표시, 범위설정, 양의 추상화, 정보의 부호화(符號化), 자료 전달 등을 위한 기초이다.

수를 표시하는 가장 기본은 단위수 또는 단위체계이다. 처음에는 셀 물건과 일대일 대응하는 단일 획들로 이루어졌는데(한자의 一·二·三, 로마 숫자의 Ⅰ·Ⅱ·Ⅲ 등), 뒤에는 다섯 또는 그 이상의 묶음을 나타내는 기호가 사용되었다(10을 나타내는 우리말의 죽, 한자의 十, 로마 숫자의 Ⅹ 등). 현재 우리가 사용하는 10진법(10기수) 체계의 기원은 고대 이집트, 바빌로니아(수메르), 중국에서 찾을 수 있다.

10진법 체계의 공적은 대부분 8~11세기 힌두-아랍 수학자들에게 있으며 근대 표기는 1202년 피사의 레오나르도(피보나치)가 발표한 〈계산판에 대한 책 Liber abaci〉에서 시작되었다.

초기 이집트인들은 10에서 10⁶까지의 거듭제곱을 각각 다른 기호로 표기한 10진법 체계를 썼지만 이것에는 자리값 표기와 0이 없었다. 비슷한 체계가 고대 중국, 그리스, 히브리 및 로마에서도 사용되었다. 한편 바빌로니아의 체계는 불완전한 60진법(60기수)의 자리 표기법이었다.

이것은 60진법에서 사용할 수 있는 60개의 서로 다른 기호를 쓰지 않고 단 두 기호를 사용해 값을 표시했기 때문에 값들을 표현하는 것이 명확하지 않아 많은 어려움을 겪었고 문맥을 분석해야만 해결되었다. 마야 체계는 명목상 20진법(20기수)이었으나 360일로 된 역법(曆法)에 맞추기 위해 연속되는 자리값이 20의 거듭제곱(20⁰=1, 20¹=20, 20²=400, 20³=8,000, 20⁴=160,000,……)이 아니라 20⁰=1, 20¹=20, 18×20¹=360, 18×20²=7,200, 18×20³=144,000……으로 변형되었다.

0을 수로서 사용한 경우가 이집트 수체계에 이따금 나타났다.

그러나 두 수 사이의 빈자리를 나타내기 위해서만 쓰였고 수 끝에는 쓰이지 않았다. 초기의 중국인들에게 0을 나타내는 기호는 없었지만 주판을 발명·사용한 것으로 보아 그들이 위치로 값을 나타내는 기수 표기와 숫자로서의 0에 대해 암묵적으로 인식했음을 보여준다. 마야인들에게 기호 0은 있었지만 기수 표기의 일관성이 없어 계산하는 데 있어 사실상 불필요했다. 위치로 값을 나타내는 기수 표기법에서 자리를 지정하는 0을 처음 쓴 사람은 아마도 무하마드 이븐 무사 알 화리즈미(780~850)였을 것이다.

0과 서부 아라비아 숫자는 주로 교황 실베스터 2세가 된 제르베르의 노력으로 10세기에 유럽 전체에 퍼져 사용하게 되었다.

측정, 분석적 정량화(定量化), 복잡한 계산이 더욱 필요하게 됨에 따라 양을 단순히 기호로 표시하던 것에서 근대적 수체계로 바뀌게 되었다. 근대 수체계의 현저한 특징은 기수 위치표기(위치값), 숫자 0, 숫자의 1보다 크거나 작은 부분을 구별하기 위해 점이나 쉼표를 사용한 것이다.

몇몇 고대 수체계는 위치의 기수 표기를 사용했지만 일관성이 없고 자주 혼돈을 일으켰다. 현대 수체계에서는 각 원소의 독립된 기호가 존재하고 그 위치가 가중값을 결정하기 때문에 수의 표현을 더욱 짧고 단순하게 표시하는 것이 가능하다. 또한 이 원리는 일반원칙이 적용되는 계산을 다른 문제로 확장하는 것을 쉽게 해준다. 0의 사용으로 계산을 위한 수의 정확한 배열이 가능해졌고 일관성있는 수 표현법이 마련되었다.

자리의 기수 표기, 0, 점을 사용하기 전에는 곱셈, 나눗셈, 근의 거듭제곱근 풀이 등의 계산은 소수의 전문가들에게 맡겨야 했다.

1100년대까지 10진법을 사용한 연산가(演算家)들은 계산속도와 정확도에서 주판을 사용한 주판사용가들을 능가했으며 결과를 영구히 기록하는 장점도 가졌다. 이러한 요소를 가진 수체계가 발달되고 널리 사용되어 천문학·제조업·항해술 같은 분야에 필요한 계산의 정확성과 용이성이 향상되었다. 결국 로그, 계산자, 기계·전기 계산기, 컴퓨터 등 자료를 처리하는 더 효율적인 형태를 이끌어냈다.

임의의 기수에 대한 일반적 수 표현은 다음과 같다.

(b는 기수, c_i와 d_i는 자리값 계수)

앞서 전개된 수는 더하기 기호와 기수의 거듭제곱 표현 없이 쓸 수 있다(즉 자리값 성질을 이용해서 c_nc_n－1……c₂c₁c₀. d₁d₂……d_n으로 쓸 수 있음). 이 표기에서 다음의 사실을 알 수 있다.

① 점에서 왼쪽으로부터 잇따른 각 숫자는 b⁰ (=1)으로 시작하는 기수의 오름차순 거듭제곱의 계수이다. ② 점에서 오른쪽으로부터 잇따른 숫자는 b^－1으로 시작하는 기수의 내림차순 거듭제곱의 계수이다. ③ 숫자는 직접 기준점 근처에 일렬로 나열할 수 있으며 기호의 순서가 어떻게 값에 영향을 미치는가를 결정하지 않고 곧바로 계산할 수 있다(로마 숫자에서는 ⅥⅩⅣ=64, ⅣⅩⅥ=46처럼 기호의 순서가 중요함) ④ 필요한 기호의 개수는 기수의 값과 같다(6진법에는 0, 1, 2, 3, 4, 5와 같은 6개의 기호가 있음). ⑤ 기호는 0에서 시작해서 기수보다 하나 작은 값으로 끝난다(0, 1, 2,……, b－1). ⑥ 기수는 개별적인 기호를 갖지 않고 항상 '10'(1×b¹＋0×b⁰)으로 표시한다.

'10'은 기수 2에서는 2, 기수 12에서는 12를 의미한다. ⑦ 수의 값은 기수의 거듭제곱과 계수의 곱의 합과 같다.

10진법 체계에서 수 983.75는 900＋80＋3＋7/10＋5/100 또는 9×10²＋8×10¹＋3×10⁰＋7×10^－1＋5×10^－2의 간결한 표현이다. 한편 수 983.75는 2진법으로 1111010111.11(1×2⁹＋1×2⁸＋1×2⁷＋1×2⁶＋1×2⁴＋1×2²＋1×2¹＋1×2⁰＋1×2^－1＋1×2^－2)이며, 8진법으로 1727.6(1×8³＋7×8²＋2×8¹＋7×8⁰＋6×8^－1)이다.

기수가 10일 때에만 곱셈없이 계수들을 수값으로 곧바로 해석한다. 앞의 예에서 다음 2가지 성질이 증명된다. ① 유리수(정수의 비로 표현할 수 있는 수)는 기수가 정수인 경우 그대로 유리수이다. ② 어떤 유리수도 유한하거나 반복하는 10진법의 소수로 표현가능하다.

토머스 해리엇(1560~1621)은 처음으로 위치 수체계를 일반화했으나 그의 연구는 공표되지 않았기 때문에 이것을 독립적으로 발전시킨 고트프리트 라이프니츠(1646~1716)에게 명성이 돌아갔다.

라이프니츠는 2진법체계의 주창자이다. 그에게 1은 신(神), 0은 무(無)를 상징한다. 2진법의 사용으로 계수형 컴퓨터의 진보는 단순화되었다. 정보를 알리기 위해 이보다 더 작은 수체계를 이용할 수는 없다. 뜻을 분별하려면 적어도 2개의 기호가 필요하기 때문이다(이 경우 0과 1). 2진법의 사용으로 10진법에서 필요한 10개 기호(0, 1, 2,……, 9)는 필요없게 되었지만 이 간소화로 수의 길이는 길어졌다. 즉 10은 2진법으로 1010, 1,866은 11101001010, 17.6875는 10001.1011이다.

이러한 이율배반성은 컴퓨터의 빠른 속도와 거대한 기억용량 덕분에 상쇄된다.

12진법은 2가지 새로운 기호, 즉 10진법의 10과 11이 더 필요하다. 12진법은 다스, 그로스(12²), 시계의 시(時)와 같은 여러 역사적 어원을 가진다. 12는 10보다 약수가 더 많으므로(2, 5, 10과 비교해 2, 3, 4, 6, 12) 많이 사용되었다.

수는 여러 방법으로 분류될 수 있다.

가장 단순한 부류는 자연수, 즉 양의 정수(1, 2, 3,……)이며 이러한 수의 음인 음수(－1,－2,－3,……)는 17세기까지는 널리 쓰이지 않았다. 자연수와 그에 대응하는 음수, 그리고 0은 함께 정수혹은 완전수를 이룬다. 유리수(분수)는 가장 일찍이 형성된 수체계로 거슬러 올라가 정수들의 비로 표현되는 수 또는 유한하거나 반복되는 소수로 정의한다(4=4/1, 22/7=3.142857……, 5/2=2.5, 1/3=0.3333……).

무리수는 정수들의 비 또는 유한하거나 반복하는 소수로 표현할 수 없다(√2=1.4142……, π=3.14159……, e=2.71828……). 유리수와 무리수를 함께 실수라 한다(실수).

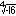
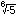
음수의 짝수근 (－3,, 등)은 실수계 원소가 아니다.

이와 같은 수를 허수라 한다. 알렉산드리아의 헤로(AD 62)가 처음으로 그 존재를 확인했으나 19세기 중반까지는 무시되거나 의미 없는 것으로 간주되었다. 허수계의 기본단위는 √－1로 i라고 쓴다. 실수와 허수 성분을 갖는 수를 복소수라 한다. 복소수는 a＋bi로 표현한다. α는 실수부분, bi는 허수부분이다.

이처럼 실수(b=0일 때) 또는 순허수(α=0일 때)는 복소수계의 부분집합이다. 순허수나 순실수의 크기와 부호는 1차원 그래프로 쉽게 나타낼 수 있다. 즉 직선 위의 점과 0(원점)에 해당하는 기준점 사이의 거리로 나타낸다. 그러나 일반적으로 복소수를 나타내려면 2차원이 필요하며, 각 복소수는 평면 위의 한 점 또는 원점에서 이 점을 향하는 선분(벡터)에 대응한다.

복소수의 2차원 그래프는 1800년경 노르웨이의 카스파 베셀과 프랑스의 장 아르강이 도입했다.

아일랜드의 수학자 윌리엄 해밀턴경(1805~65)은 곱셈의 교환공리(ab=ba)를 빼고 4개 원소(1, i, j, k)를 기저로 하는 4원수로 이름붙인 다원수계를 전개했다.

4원수는 3차원 공간에 있는 벡터의 연산에 응용될 수 있다고 증명되었지만 최근에는 미국의 과학자 J. 윌러드 깁스가 개발한 벡터 해석학 형식의 역사적 전례로 간주한다. 다차원식으로 표현되는 수와 비슷한 양(量)은 현재 수학연구의 여러 분야를 이루고 있다.→ 대수학, 벡터 해석학, 텐서 해석학, 행렬