텐서 해석학

이런 관계를 공변이라 한다.

텐서는 다양체에 관한 연구에서 생기는 기하학적 실재를 공식화하여 다루기 위해 벡터의 개념을 확장함으로써 만들어졌다.

벡터는 크기와 방향을 가진 양으로 화살표로 표시되기도 하고, 평행사변형 법칙을 따른다. 이 법칙 때문에 벡터는 성분을 갖는다(좌표계에 의존함). 좌표계가 바뀌면 벡터의 성분은 평행사변형 법칙으로부터 이끌어지는 수학적 변환법칙에 따라 변한다. 성분의 이러한 변환법칙에는 2개의 중요한 성질이 있다.

첫째, 한 특정 좌표계에서 시작하여 일련의 변형 뒤에 원래의 좌표계에서 끝나면 벡터의 성분은 시작할 때와 같다. 둘째, 벡터 사이의 관계(예를 들면 2U＋5U＝4W 와 같은 벡터 UU, V, W사이의 관계)는 좌표계에 관계없이 성분에 나타난다. 그러므로 n차원 공간에서의 벡터는 n개의 성분을 가진 양으로 보며 성분은 위의 성질을 가진 특정한 변환법칙에 따라 변환한다.

벡터 그 자체는 좌표계와 무관한 객관적 실체이나 모든 좌표계에서 대등하게 성분으로 표현된다.

텐서는 도형으로 나타냄을 강조하지 않고 벡터적 변환법칙이 일반화된 변환법칙에 따라 변하지만 2개의 주요성질을 가지는 성분을 가진 객관적 양이라고 정의한다. 편의상 좌표는 1부터 n까지의 번호를 붙이고 텐서의 각 성분은 보통 위첨자와 아래첨자를 붙인 문자로 표시하는데 이 첨자들은 각각 독립하여 1부터 n까지의 값을 취한다.

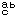
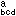
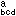
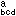
성분 T 로 표시하는 텐서는 a, b, c가 1부터 n까지의 값을 취하므로 n³개의 성분을 갖는다. 스칼라와 벡터는 텐서의 특별한 경우로 스칼라는 좌표계마다 하나의 구성성분을 갖고 벡터는 n개의 성분을 갖는다. 7R ＋2S―3T＝0과 같은 텐서 성분의 선형관계는 한 좌표계에서 유효하면 모든 좌표계에서 유효하기 때문에 그 관계는 그림으로 표현할 수는 없어도 객관적이고 좌표계와는 무관하다.

벡터의 지각분해

측도(測度) 텐서와 곡률(曲率) 텐서는 특히 중요하다.

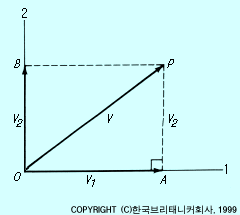
측도 텐서는 예를 들어 벡터 성분을 벡터의 크기로 바꾸는 데 사용한다. 간단히 직교좌표계의 2차원 경우를 생각해보자. 그림에서 벡터 V가 성분 V₁과 V₂를 갖는다고 하자. 직각3각형 OAP에 피타고라스 정리를 적용하면 V의 크기의 제곱은

OP²＝(V₁)²＋(V₂)²

으로 된다.

측도 텐서는 이 방정식에 감추어져 있다. 0과 1로 이루어져 있기 때문에 방정식에 나타나지 않는다. 위 식을

OP²＝1(V₁) ²＋0V₁V₂＋0V₂V₁＋1(V₂) ²

으로 다시쓰면 성분이 (1, 0, 0, 1)인 측도 텐서가 나타난다.

사선(斜線)좌표계를 사용하면 위의 OP²에 대한 공식은 일반적으로

OP²＝g₁₁ (V₁)²＋g₁₂V₁V₂＋g₂₁V₂V₁＋g₂₂ (V₂)²

이며, g₁₁, g₁₂, g₂₁, g₂₂는 측도 텐서의 새로운 성분이다.

측도 텐서로부터 곡률 텐서라는 복잡한 텐서를 만드는 것이 가능하다. 곡률 텐서는 그것이 속해 있는 n차원 공간의 내부곡률의 다양한 모습을 나타낸다.

텐서는 기하학과 물리학에 많이 응용된다. 일반상대성이론에서 아인슈타인은 물리학의 법칙은 어떤 좌표계에서도 같아야 한다고 주장했고 물리학의 법칙들을 텐서 방정식으로 표현하려고 했다.

그의 특수상대성 이론에서 시간과 공간은 불가분의 4차원 시공간을 형성한다. 아인슈타인은 중력이란 4차원 시공간의 측도 텐서로만 표시되어야 할 것이라고 가정했다. 상대론적 중력 법칙을 표현하기 위해 그는 그 법칙으로부터 형성된 측도 텐서와 곡률 텐서를 기초로 생각했다. 일단 이들 양에 국한하기로 하자 곧 중력법칙에 대한 본질적으로 유일한 텐서 방정식을 이끌었다. 여기서 중력은 힘으로서가 아니라 시공간의 곡률의 표현으로서 나타난다. 텐서는 일찍이 연구되었지만 텐서와 그 응용에 대한 수학자와 물리학자들의 폭넓은 관심을 일으키게 한 것은 아인슈타인의 일반상대성이론이다.