행렬
다른 표기 언어 matrix , 行列
요약
행렬을 이루는 각 수들은 원소 또는 성분이라고 한다. 행렬이라는 용어는 19세기 영국의 수학자 A.케일리가 도입했으며, 행과 열에 수를 나열하여 만든 행렬의 대수적 개념을 발전시켰다. 행렬곱은 차수와 순서가 다르면 결과값도 달라진다.
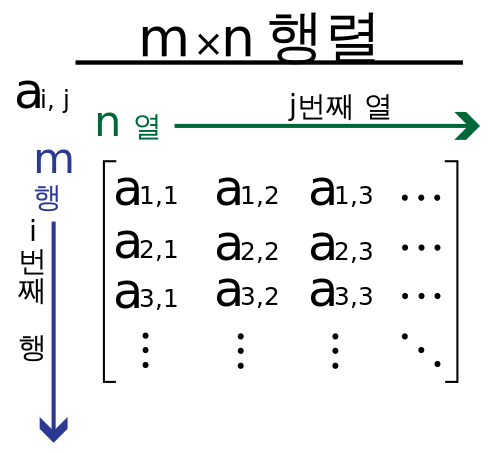
m행과 n열이 있을 때 이 행렬은 'm행 n열 행렬'이라 하고 'm×n'으로 쓴다. n행과 n열을 갖는 행렬은 n차 정방행렬이라 하는데, 보통 사용하는 숫자는 1×1 행렬로 간주하여 정수 3은 행렬 [3] 으로 생각할 수 있다.
영어 대문자로 행렬을 표기하고, 그 문자의 소문자 아래쪽에 2개의 첨자를 붙여 원소를 표시한다. 즉 aij는 행렬 A의 I행 j열에 속한 원소라고 할 수 있다. 조건에 따라 행렬을 더하거나 곱할 수 있으며 이 성질로 행렬대수라는 수학적 체계가 나온다.
각 수들을 이 행렬의 원소 또는 성분이라고 한다.
행렬은 수학의 여러 분야에서는 물론 공학·물리학·경제학·통계학 등에서 널리 응용된다. 역사적으로 처음에는 행렬이 아니라 행렬식이라는 정방행렬과 연관된 수값이 인식되었다가 점차 대수적인 것으로 행렬의 개념이 나타났다. 행렬이라는 용어는 19세기 영국의 수학자 A.케일리가 도입했는데 그는 행렬의 대수적 개념을 발달시켰다.
m행과 n열이 있을 때 이 행렬은 'm행 n열 행렬'이라고 하고 'm×n'으로 쓴다.
예를 들어
는 2×3행렬이다.
n행과 n열을 갖는 행렬은 n차 정방행렬이라 한다. 보통 사용하는 숫자는 1×1 행렬로 간주하여 정수 3은 행렬 [3] 으로 생각할 수 있다. 일상적으로 영어의 대문자로 행렬을 표기하고, 그 문자의 소문자의 아래쪽에 2개의 첨자를 붙여 원소를 표시한다. 즉 aij는 행렬 A의 I행 j열에 속한 원소라고 할 수 있다.
만일 A가 위의 예의 2×3행렬이라 하면 a11=1, a12=3, a13=8, a21=2, a22=-4, a23=5가 된다. 조건에 따라 행렬을 더하거나 곱할 수 있으며 이 성질로 행렬대수라는 중요한 수학적 체계가 나온다. 행렬은 연립방정식에서 자연스럽게 나온다. 다음과 같은 미지수 x와 y에 대한 연립방정식
2x+3y=7
3x+4y=10
에서 행렬
의 원소는 미지수 x와 y의 계수들이다.
이 연립방정식의 해는 수와 그들의 배열에 따라 달라진다. 즉 7과 10이 바뀌면 해도 달라진다.
두 행렬 A와 B에서 행의 수와 열의 수가 같고 모든 i와 j에 대해 aij=bij이면 A와 B는 같다고 한다.
A와 B가 모두 m×n행렬일 때 합 S=A+B도 m×n행렬이고 S는 원소 sij=aij+bij를 갖는다. 즉 S의 각 원소는 A와 B의 같은 위치에 있는 원소들을 더한 것과 같다. 행렬 A에 상수 c를 곱할 경우 곱은 cA나 Ac로 표기하며 각 원소는 caij이다.
행렬 A와 B를 곱하여 행렬 C를 만들 경우 첫째 행렬 A의 열의 수와 둘째 행렬 B의 행의 수가 같을 때만 정의한다. 곱한 행렬의 i행, j열인 cij는 A의 i행의 원소들과 B의 j열의 원소들을 대응하는 원소들끼리 곱한 다음 모두 합하여 얻는다.
기호로 쓰면 A가 m열을 B가 m행을 가질 때 cij=ai1b1j+ai2b2j+……+aimbmj이다. 곱행렬 C의 행의 수와 열의 수는 각각 A의 행의 수와 B의 열의 수와 같다.
보통 수의 곱셈에서는 ab=ba이나 행렬 A와 B는 곱셈에 대해 교환법칙이 성립하지 않는다. 그러나 결합법칙과 덧셈에 대한 배분법칙은 성립한다. 다시 말해 곱셈이 가능하도록 정의된 행렬의 경우 A(BC)=(AB)C, A(B+C)=AB+AC, (B+C)=BA+CA가 성립한다.
모든 원소가 0인 행렬은 영행렬(zero matrix)이라고 하며 O로 표시한다.
정방행렬 A가 주(主)대각선(왼쪽 위에서 오른쪽 아래로) 성분이 모두 1이고 나머지 원소는 모두 0인 행렬을 단위행렬이라고 하고 I 또는 In으로 표시하며 In은 행렬의 크기를 아는 이점이 있다. 행렬 B가 정방행렬이고 I와 O가 각각 B와 같은 크기의 단위행렬과 영행렬이라면 B+O=O+B=B, BI=IB=B가 성립한다.
이와같이 O와 I는 마치 보통 수의 0과 1 같은 역할을 한다. 사실 보통 수의 계산은 행렬이 모두 1×1인 행렬의 특수한 경우이다.
정방행렬 A는 행렬식이라는 값을 가지며 det A로 표기한다. 예를 들면 2×2행렬
에서 det A=ad-bc이다.
정방행렬 B가 det B≠0이면 B는 비특이(非特異 nonsingular)행렬이라고 한다. 만일 B가 비특이행렬이면 B의 역(逆 inverse)행렬 B-1가 존재하여 BB-1=B-1B=I가 된다. 행렬 A와 B를 알고 X는 모르는 경우, 방정식 AX=B에서 A가 비특이이면 A-1가 존재하므로 양쪽 방정식의 왼쪽에 A-1를 곱하여 A-1(AX)=A-1B를 얻고 A-1(AX)=(A-1A)X=IX=X가 되므로 X=A-1B가 되어 X는 유일한 해를 가진다.
n개의 미지수를 갖는 m개의 일차 연립방정식은 항상 행렬방정식 AX=B로 표시되는데 이때 A는 미지수의 계수로 이루어지는 m×n행렬이고 X는 미지변수로 구성된 n×1행렬이며, B는 방정식의 오른쪽에 나타나는 상수들로 된 n×1행렬이다. 과학의 여러 분야에서 매우 중요한 문제로 차수 n인 정방행렬 A가 주어질 때 AX=cX인 n×1행렬 X(n차원 벡터 X라고 함)를 찾는 문제가 있다.
여기서 c는 고유값(固有-eigenvalue)이라 하고 X는 고유 벡터(eigenvector)라 한다.