분자운동론

기체의 압력과 분자운동

기체분자는 다양한 속도로 운동하는데 그 기체분자들을 네모진 상자의 집단으로 분할하고, 임의의 상자 안에서 모든 분자가 거의 같은 속도로 같은 방향으로 운동하고 있다고 가정한다.

직교하는 3방향의 분자속도의 성분을 u, v, w라고 하고, 당분간 임의의 한 상자에만 주목한다. 그 상자의 분자는 속도성분 u₁, v₁, w₁을 가진다고 하고 이 상자의 분자가 밀폐용기 벽의 면적 S에 가하는 충격을 생각해보자. 그러면 이 면에 충돌하는 상자 속의 각분자(질량 m)는 u 방향의 운동이 저지될 때 그 면에 운동량 mu를 가하고, 또 반발되면 반대방향으로 운동량을 얻기 때문에 각 분자가 벽에 전달하는 전체 운동량은 2mu이다.

작은 시간간격 dt 사이에 S에 충돌하는 상자 속의 분자수는 이 시간간격의 초기에 거리 u₁dt 이내에 있었던 수, 즉 부피 Su₁dt 인 얇은 판 내부에 있었던 수와 같다. 상자에 들어 있는 단위부피당 분자수를 v₁개라고 하면 판 내부의 분자수는 Su₁v₁dt이다.

이 분자들은 경계벽의 면적 S에 운동량 2mu₁²v₁Sdt를 전달하기 때문에, 모든 상자 안의 분자에 의해서 전달되는 전체 운동량은

2mSdt(ν₁u₁²＋ν₂u₂²＋……)

이 된다.

여기에서 합은 S로 향하는 성분 u를 지니고 운동하는 분자를 가진 각각의 상자에 해당하는 항을 포함한다. 이 합은 1/2νU² 이라고도 한다. 여기에서 ν는 단위부피당 분자의 수를, U² 은 각분자의 u² 의 평균값을 나타낸다. 인수 1/2이 붙어 있는 이유는, 모든 상자의 절반은 S로부터 멀어지는 방향으로 성분 u를 가지고 운동하는 까닭에 S에 대한 압력에는 기여하지 않기 때문이다.

그리고 모든 분자에 대한 속도의 제곱 u²＋v²＋w²의 평균치를 C²으로 놓으면 다수의 분자가 각각의 방향으로 똑같은 운동을 하고 있기 때문에 u²,v²,w²의 평균값은 같고, 그 값은 U²=1/3C²이다.

따라서 시간간격 dt 사이에 S에 전달되는 운동량은 1/3mνSC²dt가 된다.

벽에 미치는 단위면적당의 힘, 즉 압력을 p라고 하면 전달된 운동량은 pSdt와 같지 않으면 안 되기 때문에 p의 값은

p=1/3mνC² ①

이 성립한다.

여기에서 mv는 단위부피 내의 전체질량이고, 따라서 단위체적당 질량을 단위로 해서 표시한 밀도ρ와 같기 때문에

p=1/3ρC² ②

으로 쓸 수 있다.

p와ρ는 임의의 기체에 대하여 측정할 수 있기 때문에, C 의 값을 계산할 수 있다. C 는 분자의 속도의 제곱 평균제곱근이다.

기체법칙과 분자운동

기체가 온도변화 없이 압축될 때 압력은 밀도에 비례해서 증가한다는 것이 로버트 보일에 의해서 발견되었다. 이 결론은 식 ②에서 C²이 온도에만 의존한다고 가정하면 얻어진다.

더욱이 J. A. C. 샤를과 조제프 루이 게이 뤼삭은 기체가 압력을 일정하게 유지하면서 가열되면 그 부피는 온도가 증가함에 따라 일정한 비율로 증가한다는 것을 증명해보였다.

열역학적 절대온도를 사용해서 표현하면, 압력이 일정할 때 부피는 절대온도 T에 비례하여 증가한다. 즉 실험에 의해서 확립된 기체의 법칙은 단일식p=ρRT ③로 표현될 수 있는 것이다. 여기서 R은 기체의 종류에 의존하는 상수이다.

식 ③은 보통pV=RT ④와 같이 쓰여진다. 여기서 V는 1/ρ 같고, 단위질량당 부피를 나타낸다. 식 ②와 식 ③에서C²=3RT ⑤가 얻어진다. 그러므로 각분자의 평균속력(정확하게는 속도의 제곱 평균 제곱근)은 절대온도의 제곱근에 비례해서 변화한다. 식 ③ 또는 ④를 만족하는 기체를 이상기체라 한다(→ 이상기체).

비열 단위와 기체의 분자운동

부피 안에 있는 모든 분자의 병진운동의 전체 운동 에너지는 ν(1/2mC²), 즉 1/2ρC² 또는 3/2ρRT이다.

ρ는 단위부피당 질량을 나타내기 때문에 단위질량당 에너지는 3/2RT 이다. 온도가 1℃(=1K) 증가하면 이 에너지는 3/2R만큼 증가한다. 즉 분자가 병진운동 이외의 가변 에너지를 포함하지 않으면, 기체의 정적비열은 3/2R이다. 분자가 단일원자로 이루어진 헬륨 등의 비활성기체에서 정적비열은 3/2R이라는 것이 실험에 의해서 밝혀졌다.

다원자 분자의 기체인 경우 극저온 이외에서는 정적비열이 3/2R을 넘는다. 이 차이의 원인은 다원자 분자의 회전 에너지가 그 원자의 진동 에너지의 존재로 돌릴 수 있다.

에너지 균등분배법칙과 기체의 분자운동

에너지 균등분배법칙에 의하면, 어떤 역학계가 어떤 온도에서 통계적으로 평형상태에 있을 때는 각각의 자유도, 즉 계의 각각의 독립적인 운동방식에 같은 양의 평균 운동 에너지가 분배된다. 병진운동을 하고 있는 분자는 3개의 서로 직교하는 방향으로 독립적으로 운동할 수 있기 때문에 3개의 자유도를 가지고 있다. 여러 종류의 분자로 이루어진 기체에서는 분자의 평균 병진 에너지, 즉 1/2>mC²의 값은 모든 종류의 분자에 대해서 동일하지 않으면 안 된다.

분자가 실제로 혼합되었을 때 이 결론은 분자끼리의 충돌의 효과를 분석하면 검증될 수 있다.

C²은 절대온도에 비례한다는 것이 밝혀졌기 때문에 분자의 평균 병진 에너지는 다음과 같이 쓸 수 있다.

1/2mC²=3/2kT

여기서 k는 비례상수이다. 에너지 균등분배법칙에 의하면 각 자유도에 대한 평균 운동 에너지는 1/2mC²의 1/3, 즉 1/2kT이다. 식 ⑤에 의해서 k=mR임을 알 수 있다.

k는 볼츠만 상수 또는 '한 분자당의 기체상수'라고 부르는데, 그 값은 cgs 단위계에서는 1.38065×10^－16erg/K이다. 그러나 1925년 후에 곧 고전역학의 법칙은 하나의 근사치에 지나지 않다는 것이 알려지게 되었다. 기체의 압력 계산에 사용되는 고전적 법칙은 기체분자의 병진운동의 기술에는 충분하지만, 분자의 회전운동과 진동운동을 다루는 데는 적합하지 않다. 다원자 분자로 구성된 기체의 비열의 적절한 이론은 새로운 양자역학이나 파동역학에 바탕을 두지 않으면 안 된다.

기체 분자운동론과 분자수의 계산

어떤 온도에서 1/2mC²이라는 양은 모든 기체에 대해서 동일하기 때문에, 식 ①에 의해서 단위부피 내의 분자수, 즉 ν는 동일한 온도와 압력하에서는 모든 기체에 대해 동일하다는 결론이 나온다.

이것은 아보가드로 법칙으로 알려져 있다.

기체분자 운동론에는 ν의 수치를 확인하는 확실한 방법이 없지만, 가장 좋은 방법은 전기분해에서 각 수소원자가 전자의 전하와 같은 크기의 전하를 운반한다고 하는 확립된 사실에서 출발하는 것이다. 전해액 내에서 이온화되어 있는 수소 1g이 만들어내는 전체 전기량도 알려져 있다. 1g의 전기량을 1원자의 전기량으로 나누면 수소 1g의 원자수가 얻어진다.

이 수는 수소기체 2g의 분자수와 같으며, 표준상태에서 22.4l의 부피를 차지한다. 이 분자수는 N₀=6.02×10²³의 값을 가진다.

기체의 분자운동 속도의 분포

기체의 분자가 모두 같은 속도로 운동하는 것은 아니다. 기체가 정지해 있고 교란을 받지 않을 경우, 분자속도는 제임스 클럭 맥스웰과 루트비히 볼츠만이 보인 것처럼 분자의 충돌효과에 따라, 어떤 일정한 함수에 따라 분포하게 된다.

u, v, w를 공간 내에서 직교하는 3방향에서의 속도의 성분으로 놓으면, 속도의 u 성분이 u와 u＋du 사이에 있고, v성분이 v와 v＋dv 사이에 있고, w성분이 w와 w＋dw 사이에 있는 분자수는

로 주어진다. 여기에서 N은 분자의 총수, m은 각 분자의 질량, h는 온도에 의존하는 상수이다.

이 법칙은 보통 맥스웰 속도분포법칙으로 알려져 있다.

만일 속도의 임의의 한 성분, 예를 들면 u에만 주의를 돌리고 v와 w를 무시하면, 이 성분이 u와 du 사이에 있는 분자수는

이다.

많은 문제에서는 분자속도의 각 성분보다도 속도의 크기, 즉 속력이 더 큰 의미를 지니고 있다. u²＋v²＋w²을 c²이라고 쓰면 c는 속력이고 c가 c와 c＋dc 사이에 있는 전체 분자수는 식 ⑥에서

가 됨을 유도할 수 있다.

분자수는 c의 값이 매우 클 때나 매우 작을 때에는 아주 작고, c가 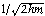일 때 최대가 된다.

식 ⑧을 적분하면 앞에서 C²로 표시된 분자속도의 제곱의 평균값도 3/2hm과 같다는 것이 드러난다. 또한 1/2mC²는 볼츠만 상수와 절대온도를 사용해서 나타내면 3/2kT와 같기 때문에

이 성립됨을 알 수 있다.

돌턴의 법칙과 기체의 분자운동론

어떤 기체가 여러 종류의 기체 혼합체이고 단위부피 중에, 예를 들면 한 종류의 기체가 질량 ρ₁ , 다른 한 종류의 기체가 질량 ρ₂만큼 포함되어 있다고 가정하자, 첫번째 기체가 경계벽에 미치는 압력은 P₁, 2번째 기체가 미치는 압력은 P₂, 서로 다른 종류의 분자들 사이에 상호작용이 없다고 가정하면 기체 전체가 미치는 압력은

P=P₁＋P₂＋……

과 같이 된다. 이 식에 따라 혼합기체의 압력은 각각의 성분기체가 혼자 존재할 때에 개별적으로 미치는 압력(분압)의 총합이라는 것이 드러난다.

브라운 운동과 기체의 분자운동론

볼츠만 상수의 값에서 질량 10^－12g의 분자 또는 분자집단은 0℃에서 2㎜/s의 평균속력을 가진다는 것이 쉽게 계산된다. 따라서 0℃의 공기 또는 액체 중에 10^－12g의 질량을 가진 입자를 넣으면 주위의 분자나 입자와의 연속적인 충돌에 의해서 이 입자는 앞에서 말한 평균속력을 얻게 된다.

이러한 질량의 입자는 현미경으로 쉽게 관측될 수 있고, 2㎜/s라는 속력도 충분히 긴 시간 동안 관측을 계속하면 확인할 수 있다. 다만 충돌할 때마다 입자의 운동이 변화하여 운동변화가 매우 빈번하게 나타나기 때문에 개개의 운동을 따로따로 관측하는 것은 불가능하다. 그렇지만 이 개개의 짧은 운동의 집합으로부터 입자는 어떤 평균속력을 가지고 운동한다는 것이 밝혀질 수 있다. 이 평균속력은 2㎜/s보다 훨씬 느리지만 현미경 관측은 가능하다.

알베르트 아인슈타인은, 이론적으로 예측된 이 운동이 이미 1827년 식물학자 로버트 브라운에 의해서 처음으로 관측된 '브라운 운동'과 같다는 것을 보였다. 이 운동의 관측으로부터 ν와 N₀의 값이 도출되는데, 이 값은 앞에서 서술한 방법에 의해서 얻어진 것과 상당히 일치한다. 이렇게 해서 브라운 운동은 분자운동론에 의해서 가정된 열운동의 실재성을 눈에 보이는 형태로 증명했던 것이다.

기체상태방정식의 보정

돌턴의 법칙, 브라운 운동 등 기체의 분자운동에 대해 서술한 법칙은 밀도가 너무 높지 않거나 온도가 너무 낮지 않은 모든 기체에 대해서는 꽤 잘 들어맞지만, 완전히 정확하다고 말할 수는 없다.

반 데르 발스는 1873년에 압력에 대한 식 ③ 또는 ④의 불완전성의 원인으로 다음 2가지를 들었다. 첫째, 계산에는 분자가 유한한 크기를 가진다는 것과 그결과 분자의 운동이 서로 방해한다는 것이 고려되지 않았다. 둘째, 계산에는 작지만 실재한다는 것이 알려져 있는 분자간의 인력이 고려되지 않았다. 이 힘이 존재하면 분자가 벽에 도달했을 때 벽과의 충돌에 기인하는 힘 이외의 힘도 분자에 작용하게 된다.

반 데르 발스는 첫번째 요인을 고려하기 위해서 분자가 강체 탄상구라고 가정하고, 식 ④의 V를 V－b로 바꾸지 않으면 안 된다는 것을 발견했다.

여기에서 b는 단위질량 속의 전체분자가 차지하는 부피의 4배이다. 또 2번째 요인을 고려하기 위해서는 인력이 약하다고 하는 가정에 기초하여 p를 p＋(a/V²)으로 바꾸었다. 여기서 a는 새로운 상수이다. 이렇게 해서 그는 압력-부피 관계에 대해서 반데르발스의 상태방정식이라고 알려진 관계식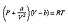를 얻었다. 이 식은 고압하에서의 기체의 일반적인 행동을 예측한다고 하는 커다란 장점을 지니고 있다.

기체 내 분자의 자유행로

기체 내의 각 분자를 작은 공으로 보기로 하자. 각각의 작은 공은 직선상을 진행하여 어떤 표적에 충돌하며, 그후 속도와 운동 방향이 바뀐다. 어떤 분자는 기체가 들어 있는 용기의 벽에 충돌하고, 또 어떤 분자는 다른 분자와 충돌한다.

자유행로의 분포

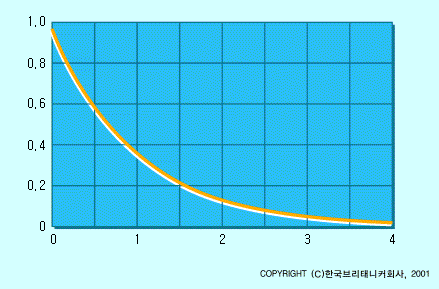
각 분자의 지름을 σ라고 하면 2개의 분자의 중심간의 거리가 σ 이하로 접근할 때 반드시 충돌한다. 따라서 각 분자는 면적이 πσ²인 표적을 형성한다고 생각할 수 있다.

단위부피 중에 ν개의 분자가 존재할 경우, 두께 t, 단면적 S의 얇은 층 안의 분자수는 νtS이고, 이 분자들은 전체면적이 πσ²νtS인 표적을 형성한다. 이 양은 t에 비례하고 t 가 어떤 특정한 값을 가질 때 S와 같아진다. 다시 말해 t 가 어떤 확정된 값을 취할 때 S와 같아진다.

t 가 이 값을 가질 때 층을 구성하고 있는 분자로 형성된 표적은 정확하게 전체면적 S를 채우기 때문에 분자는 이 층을 통과하는 동안에 반드시 충돌하게 된다. πσ²νtS와 S가 같아지는 t의 값은 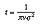이다.

그러나 앞에서 보인 간단한 계산은 몇 가지 점에서 수정이 필요하다. 분자는 공간에 불규칙하게 분포되어 있으며, 분자의 속도변화도 고려하지 않으면 안된다. 맥스웰에 의해서 처음으로 행해졌던 엄밀한 계산에 의하면, 분자가 다른 분자와 충돌할 때까지 진행하는 평균거리 l은 에 의해 주어진다.

충돌 사이의 각각의 자유행로는 평균자유행로 l의 양쪽에 통계적으로 분포해 있다. 자유행로의 빈도가 최대로 되는 거리는 실제로 0이다. 이 경우 하나의 분자는 다른 분자가 충돌할 때까지 거의 정지해 있다. 어떤 일정한 길이의 자유행로의 빈도는 길이가 증대함에 따라 감소하고, 평균길이 l의 수배의 길이를 가진 행로의 빈도는 아주 적다.

열전도와 기체의 분자운동론

분자가 다른 분자와 충돌하면 에너지를 얻거나 잃는데, 자유행로를 기술할 때에는 분자의 에너지는 변하지 않는 것으로 가정했다. 온도가 균일하지 않은 기체 중의 분자의 운동을 생각하기로 하자. 기체의 하나의 층 AB의 온도를 T, 평균자유행로 l만큼 떨어진 또 하나의 평행층 A'B'의 온도를 T'로 놓자. 온도차 때문에 2개의 층 내에 있는 분자의 평균 에너지는 서로 다르다. 이 에너지를 각각 E와 E'라고 하자. A에서 충돌로부터 출발하여 A'에서의 충돌까지 자유행로 AA'를 그리는 분자는 평균적으로 층 AB 고유의 에너지 E를 가지며, 반대방향으로 자유행로 B'B를 그리는 분자는 평균적으로 층 A'B'고유의 에너지 E'을 가지게 된다. T가 T'보다 높으면 E는 E'보다 크며, 따라서 뜨거운 층 AB에서 차가운 층 A'B'의 방향으로 그 반대방향보다 더 큰 에너지가 운반되게 된다. 결과적으로 기체의 뜨거운 부분에서 찬 부분으로 열 에너지의 흐름이 일어나는 것이다. 이렇게 해서 기체에서의 열전도가 분자운동론에 의해서 설명되는 것이다. 열전도도 K는 다음 식으로 주어진다.

기체열전도

K=1/3ρC_vcl ⑩

여기서 ρ는 밀도, C_v는 기체의 정적 비열, C'는 평균속력, l은 평균자유행로이다.

점성 기체와 분자운동

점성의 현상도 같은 방식으로 논할 수 있다. 기체의 층 AB와 A'B'이 P와 평행하고, 속도 V, V'로 움직이고 있다고 하면, 층 AB 내의 분자는 평균적으로 AB에 평행한 운동량 mv를 가진다.

평면 PQ를 가로질러서 일어나는 운동량 mv의 전달을 생각하면 점성도 μ는

μ=1/3ρcl ⑪

에 의해 주어진다. 식 ⑩과 ⑪은 열전도도, 점성도 및 정적비열 사이에 K=μC_v라고 하는 흥미있는 관계를 제공한다. 구형분자에 대해서는 충분히 보정한 값으로서

K=5/2μC_v

가 성립한다.

확산과 기체의 분자운동

확산 현상도 비슷한 방식으로 취급될 수 있다. 두 종류의 기체 G₁과 G₂를 가정하고, AB에서 G₁의 농도를 θ, A'B'에서 G₁의 농도를 θ라고 하자.

자유행로 AA'를 그리는 분자가 G₁의 분자일 확률이 θ이기 때문에, 이 자유행로를 그리는 각 분자가 수송하는 기체 G₁의 질량은 '평균적으로' θm과 같다.

평면 PQ를 가로질러서 단위시간당 운반되는 G₁의 순수 수송량으로부터 확산계수 D가 다음과 같이 얻어진다.

D=13cl

고체 및 액체의 분자운동론

고체상태

고체에 있어서 분자는 상호 인력 및 반발력에 의해 매우 견고하게 유지되고 있기 때문에 분자가 그 평형위치에서 벗어나 움직이는 일이 거의 없다.

우리가 일상적으로 경험하는 많은 사실을 이것으로 설명할 수 있다. 예를 들면 미세하게 조각된 금속의 표면은 (철강조각에 사용되는 판금처럼) 여러 세기 동안 정확한 형상을 유지하고 있으며, 또한 금속 물체를 금박으로 씌워도 금 원자는 어디까지나 표면에 머물러 있다. 만약 금 원자가 아주 미세한 거리에서 이동한다면, 결국 금 원자는 밑에 있는 금속의 원자와 섞이어 내부로 확산될 것이다.

고체를 구성하고 있는 분자의 집합은 가벼운 용수철로 연결된 무거운 입자의 집합에 비유되며, 분자 간의 결합은 각각의 용수철이 인접 입자들을 결합시키고 있는 것과 닮아 있다.

만약 그대로 둔다면 각각의 입자는 평형위치로 되돌아간다. 외부의 힘을 가하면 입자의 집합 전체가 압축되거나 팽창되거나 혹은 뒤틀리거나 하는데 이는 고체의 성질과 똑같다.

지금 2개의 분자를 같은 점에서 실로 연결하고, 그 중 1개를 좌우로 당기어 다른 1개에 충돌시켰다고 하자. 충돌 후 2개의 분자 덩어리는 반발하고, 그와 같은 과정이 몇 번 되풀이된 뒤 2개의 분자 덩어리가 반발하며, 마지막에는 2개의 분자 덩어리가 다시 접촉하여 매달려 있게 될 것이다.

최초의 충돌에서는 충돌의 충격을 받는 표면 분자층이 그 배후에 있는 분자층으로 밀려나간다. 그 배후에 있는 층은 이때문에 운동을 받게 되고 다시 뒤에 있는 층에 영향을 미치며, 계속 이와 같은 작용이 되풀이된다. 따라서 충돌로 인해 분자 덩어리 내에 있는 모든 분자가 운동을 받아 덩어리가 서로 충돌하는 것을 멈출 때까지 덩어리를 구성하고 있는 분자는 그 평형위치 주위에서 진동할 것이다. 이 덩어리가 충돌 전에 갖고 있던 에너지는 분자 덩어리를 구성하는 개개 분자의 미소운동의 운동 에너지 및 위치 에너지로 표현된다.

이와 같이 통상적인 경험이 보여주듯이 2개의 물체가 충돌하면 물체의 거시적 운동으로 잃는 운동 에너지는 실제로는 열 에너지로 변환되는 것이다.

다시 서로 접촉하고 있는 2개의 물체를 상상하고, 한쪽 표면을 다른 한쪽의 표면으로 마찰한다고 해 보자. 2개의 물체의 표면층의 분자는 상호 힘이 미치기 때문에, 마찰을 하면 각각의 층은 다른 층의 분자에게 운동을 주고 마찰에 투입된 열 에너지는 이 운동을 일으키는 데에 사용된다.

이와 같이 하여 마찰에 의한 열 발생 현상이 설명된다. 처음에는 열운동은 2개의 물체의 마찰면 가까이에 있는 분자에 한정되어 있지만, 결국 내부의 분자도 운동을 받아 최종적으로는 물체 전체로 열운동이 확산된다. 이것은 열전도의 한 예이나 이것만으로 열전도 현상의 모든 것이 설명되는 것은 아니다. 왜냐하면 특히 전기 전도체에 있어서는 다른 과정도 열전도에 기여하기 때문이다.

고체 분자가 평형위치 주위에서 진동하고 있을 때 분자 간의 평균거리가 분자가 정지하고 있을 때의 것과 같아야만 할 이유는 없다.

이것은 일반적으로 물질의 온도 변화에 따라 길이가 변화한다고 하는 사실을 설명한다. 예를 들면 2개의 분자가 정지하여 평균상태에 있을 때 거리가 a만큼 떨어져 있다고 하자. 거리가 이보다 작아지면 서로에게 미치는 반발력이 인력 시간에 걸쳐 평균을 이룬 두 분자의 평균거리는 a보다 커질 것이다. 이러한 종류의 분자로 구성된 물체이면 가열에 의해 팽창한다.

물체의 온도가 상승하면 분자의 평균 에너지가 증대하여 분자의 평형위치에서의 변위의 범위도 또한 증대한다.

어떤 온도에서 준자가 평형위치에서 아주 먼 거리까지 진동으로 변위하여 원래로 돌아오지 않고 새로운 평형위치에 들어가 그 주위에서 진동하는 일이 빈번히 일어나는 단계에 도달하는 것을 생각할 수 있다. 고온의 고체내에서 일어나는 더딘 확산 과정은 이와 같이 설명된다. 또한 만약 분자가 아주 간단하게 위치를 바꾼다면 물체의 형상이 변화할 수 있다. 즉 물질이 소성을 가진다. 마지막으로 분자의 운동 에너지가 너무 커서 분자간에 끊임없이 위치의 재배열이 행해질 때에는 그 물질은 완전한 액체 상태에 도달한다.

그러나 결정 고체는 가소적으로 되지는 않고 결정의 표면이 점차 융해하는 과정에 의해 직접 액체상태로 이행된다고 보여진다.

고체상태의 이론

만약 고체를 구성하고 있는 분자가 용수철로 연결된 무거운 입자의 집합과 유사하여, 그에 따라 각 분자에 미치는 주요힘이 인접 분자에 대한 평형위치로부터의 변위에 비례한다고 하면 분자의 불규칙한 열운동으로 용수철을 늘리거나 오므리거나 할 때와 같이 분자는 위치 에너지를 갖게 된다.

뉴턴의 운동법칙에 의하면 이 위치 에너지의 평균값은 분자의 병진 운동 에너지의 평균치와 같다. 또한 에너지 균등분배법칙에 의하면 병진의 평균 운동 에너지는 모든 분자에 대해 같다. 이러한 점 때문에 고체내의 단원자 분자는 위치 에너지를 갖지 않는 기체내에서의 수치의 2배의 열 에너지를 갖게 되는 것이다.

이와 같이 하여 단일 화학 원소로 이루어지는 고체의 일정수의 분자를 1℃ 상승시키는 데 필요한 열량은 거의 대부분의 원소에 대해 거의 동일하며, 또 헬륨과 같은 기체를 구성하고 있는 같은 수의 분자에 대해 필요한 열량의 2배라고 하는 법칙이 설명된다.

그러나 이 법칙에는 예를 들면 다이아몬드형 구조에 있어서의 탄소와 같은 현저한 예외가 있다. 근래에 들어 온도를 충분히 낮게 하면 필요한 열량은 모든 물질에서 감소하여 절대 온도가 낮아짐에 따라 거의 0이 되는 것이 발견되었다. 이 에너지 균등분배법칙의 파탄에 대한 수학적 설명은 양자역학에서 얻을 수 있지만 이 새 이론에서는 분자의 운동에 관한 구체적인 기술을 할 수가 없게 된다.

전술한 법칙이 성립하는 고체의 경우 각 분자는 단일 원자로 구성되어 있다.

많은 간단한 화학 화합물의 원자도 또한 고체 상태에 있어서의 독립 단위로서 결정 구조를 구성한다. 예를 들면 소금의 분자는 2개의 원자 즉 나트륨 1개와 염소 1개를 포함하는데, 소금 결정에 있어서는 나트륨 각 원자가 하는 일이 없도록 규칙적인 결정격자로 배열되어 있다. 이와 같은 결정은 1개의 거대 분자를 구성하고 있다고 할 수 있다. 그러나 다른 물질의 결정에 있어서는 원자가 이온이나 분자에 꽉 짜여져 있다. 이와 같은 결정의 열운동은 이온 또는 분자 전체의 운동과 분자 가운데 원자의 진동으로 분해할 수가 있다.