극한

극한

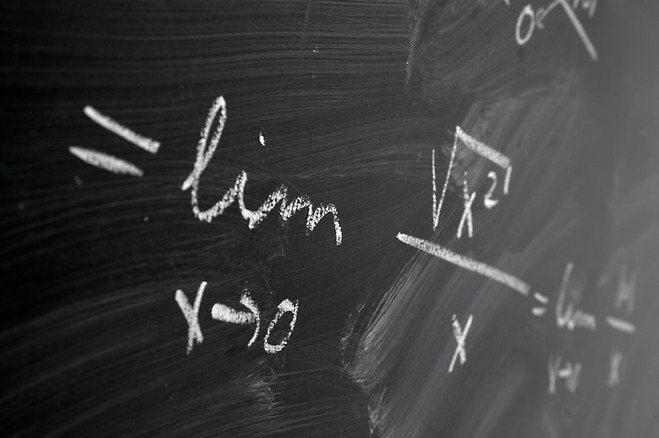
함수값이 정의되지 않는 점에서 그 점 부근의 함수값과 모순되지 않는 값을 얻기 위해서 주로 사용한다. 예를 들어 함수 (x²－1)/(x－1)은 x=1일 경우에는 0으로 나누게 되어 연산이 불가능하므로 함수값이 정의되지 않는다. 다른 모든 x값에서는 분자를 인수분해한 뒤에 (x－1)로 나누면 (x＋1)을 갖는다.

이것은 1을 제외한 모든 x값에 대한 앞의 분수식과 같으며, x=1일 때 값이 정의되지 않았던 것과는 달리 함수값은 2가 된다. 2라는 값은 함수 (x²－1)/(x－1)에서 x=1일 때의 값이 아니고 x가 1에 가까워질 때의 극한값이다.

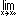
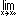
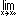
점 x₀에서 함수 f(x)의 극한은 f(x)로 쓰며 정의하는 방법은 다음과 같다. 점x₀를 제외하고 x₀를 포함하는 어떤 구간에서는 g(x)=f(x)이고 끊어지지 않은 연속함수 g(x)가 있다면, f(x)=g(x₀)이다. 극한에 대한 더 근본적인 개념을 연속성 개념에 관계없이 f(x)=L이라 정의할 수 있다.

즉 원하는 접근정도 ε에 대해 x₀주변에서 구간을 찾아 그 구간 안에서 계산한 모든 f(x)의 값과 L과의 차이는 ε보다 작게 되어야 한다. 즉,│x－x│＜δ일 때 │f(x)－L│＜ε이다. 후자의 정의는 주어진 수가 실제로 극한값인가 아닌가를 가려낼 수 있으나, 처음 정의는 극한값을 찾는 방법을 준다. 극한, 특히 분수식의 극한을 계산할 때는 더 명백하게 쓰기 위해 대부분 함수를 변형하는데, 앞의 (x²－1)/(x－1)이 그 예이다.

극한은 함수의 도함수나 변화율을 계산하는 방법이며 근사값을 정확한 양으로 만드는, 예를 들면 곡선으로 둘러싸인 영역의 면적을 구분 구적하여 얻어진 근사값의 극한으로 정의하는 것과 같은 방법처럼 해석학 전반에서 널리 사용된다.