확률

정의

먼저 간단한 예를 들어보자. 가령 동전던지기에서 동전이 비뚤어지지만 않는다면 앞이 나올 확률과 뒤가 나올 확률은 같다고 할 수 있다.

이때 앞이 나오는 것과 뒤가 나오는 것을 각각 하나의 사건이라고 하는데, 이들 사건의 확률은 각각 1/2이다. 다른 예를 들어보자. 각각 a, b, c, d의 글자가 씌어진 같은 모양의 판이 4장 있다. 이것들을 일렬로 나열할 때 나열하는 조작은 우연현상이라고 할 수 있다. 나열하는 방식은 전부 4!=4×3×2×1=24종류가 있으므로 특정한 나열방식, 가령 a, b, c, d순으로 나열될 확률은 1/24이다.

또 a가 맨 앞에 나열되는 경우는 3!=6가지이므로 이같은 사건의 확률은 6/24=1/4이 된다. 마찬가지로 b, c 또는 d가 맨 처음 나열될 확률도 모두 1/4이다.

이러한 예에서처럼 전체 n가지의 가능성이 있고 어느 것이나 같은 정도로 기대할 수 있다고 하자. 이때 지정된 조건에 맞는 경우가 m가지라면, 이 조건이 충족되는 확률 p는 p=m/n이라고 정의할 수 있다.

여기서 n가지 개개의 경우를 기본사건이라고 부르고 몇 개의 기본사건이 모인 집합을 사건이라고 한다. 한 사건이 m개의 기본사건으로 되어 있을 때 이 사건의 확률은 앞서 말한 p=m/n이 된다. 수학적으로 좀더 엄밀하게 정의하려면, 1933년 소련의 A. N. 콜모고로프가 제창한 공리계를 따른다.

기본사건을 w 등으로 표시하고 이들 전체의 집합을 Ω라고 하자. 취급하고 싶은 사건(Ω의 부분집합)의 집합을 B로 표시할 때 이B는 전체사건 Ω를 포함하고 가산합집합과 여집합을 취하는 연산에 대해 닫혀 있어야 한다.

즉 B에 속한 사건 A₁, A₂……가 있으면 그 가산합사건 A₁∪A₂∪……도 B의 원소가 되어야 하고 B에 속한 어떠한 사건 A에 대해서도 그 여집합 A=Ω－A도 B에 속해야 한다.

A는 사건 A의 여사건이라고 한다.

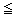
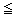
또 ① B의 각 사건 A에 대해 그의 확률인 수 P(A)가 대응하여 0P（A）1이고, ② 전사건 Ω는 P(Ω)=1이며, ③ P는 가산가법성을 만족한다.

즉 사건 A, B의 공통집합이 공집합일 때 이들 둘은 배반사건이라 하는데, 배반사건의 열 A₁, A₂,……가 주어졌다고 하면 이들의 가산합사건 A=A₁∪A₂∪……의 확률은 각 사건 확률의 합과 같다. 수식으로 쓰면

P(A)=P(A₁)＋P(A₂)＋……

이다.

이러한 성질을 가진 조(Ω, B, P)를 확률공간이라고 한다. 여기서 P는 해석학에서 측도라고 부르는 것과 같은데 특별히 P(Ω)=1이다. 주사위를 2개 던지는 예를 들어보자. 눈이 나오는 가지수는 6×6=36가지가 있는데 나온 가지 수의 순서쌍을 (1, 1), (1, 2), ……, (2, 1), (2, 2), ……, (6, 6)이라고 적었을 때 이들 각각을 기본사건이라고 한다. 전체를 Ω로 하고 B는 Ω의 부분집합 전체로 구성된 가장 상세한 것을 취한다.

사건 A(∈B)의 확률은 P(A)=#(A)/36로 한다. 여기서 #(A)는 A에 포함되는 기본사건의 개수를 나타낸다. 예를 들어 나온 눈의 합이 4가 되는 사건은 (1, 3), (2, 2), (3, 1)이며, 그 확률은 3/36=1/12이다.

이 예에서 첫째 주사위에 나오는 눈이 1인 사건 A는 (1, 1), (1, 2), ……, (1, 6)이며 2번째 주사위에 나온 눈이 3인 사건 B는 (1, 3), (2, 3), ……, (6, 3)이다.

A∩B는 단 하나의 기본사건 (1, 3)으로 그 확률은 1/36이다. P(A)=P(B)=6/36=1/6에 주의하면 다음과 같은 등식이 성립한다.

P(A∩B)=P(A)P(B)

이 경우 A와 B는 독립이라고 한다.

여러 개의 사건 A₁, A₂, ……가 있을 때, 이들로부터 몇 개를 마음대로 고른 A_i,A_j, ……, A_k에 대하여 항상

P(A_i∩A_j ∩ …… ∩A_k)

=P(A_i) P(A_j) …… P(A_k)

가 성립하면 원래의 사건계는 독립이라고 한다.

시행

주사위를 던지는 경우에서와 같이 결과는 우연하고 배반사건의 열 A₁, A₂, ……가 있어서 이들 중 어느 1가지가 반드시 일어날 때, 즉 P(A₁)＋P(A₂)＋……=1일 때 이러한 행위를 시행이라고 한다.

2개의 시행을 각각 T₁, T₂라고 쓰고 이들 둘에는 각각 배반사건의 열 A₁, A₂, ……와 B₁, B₂, ……가 있다고 하자.

만약 임의로 고른 A_i와B_j가 독립이라면, 즉 P(A_i∩B_j)=P(A_i)P(B_j)라면 시행 T₁과 T₂는 독립이라고 한다.

예를 들면 주사위나 동전을 2번 던지는 경우가 여기에 해당된다. 독립된 시행은 몇 번이라도 반복할 수 있다. 특히 매번 똑같이 시행되고 2가지 실현가능성밖에 없을 때 이를 베르누이 시행이라고 한다. 대응하는 배반사건은 2가지, A₁과 A₂(A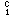)뿐이다.

이들을 각각 성공·실패라고 하며 확률은 각각 P와 q(=1－p)로 나타내는 경우가 많다.

조건부 확률

2가지 사건 A, B가 있을 때, 이들 둘은 다음 4가지로 생각할 수 있다.

확률

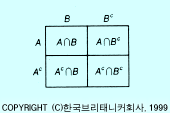
① A와 B가 일어난다.

② A가 일어나고 B는 일어나지 않는다. ③ A는 일어나지 않고 B가 일어난다. ④ A도 B도 일어나지 않는다. 여사건 A^c, B^c를 사용해서 위의 각 경우를 사건으로 나타내면, 각각 ① A∩B, ② A∩B^c, ③ A^c∩B, ④ A^c∩B^c이 된다.

A가 일어났을 경우를 가정해 보면 가능성이 있는 것은 ①과 ②의 경우뿐이다. 관점을 바꾸어 A를 전체사건이라고 생각하면 여기서 B와 B^c이 차지하는 비율은 각각 P(A∩B)와 P(A∩B^c)에 비례하기 때문에 전체사건의 확률을 1로 하면, A가 일어났을 때 B, B^c의 조건부 확률은,

P_A(B)=P(A∩B)/P(A),

P_A(B^c)=P(A∩B^c)/P(A)

이다(당연히 P(A)=0일 때는 제외). 기호 P_A(B)는 P(B/A)라고도 쓰며 이 기호를 이용하면 A와 B가 일어날 확률, 즉 P(A∩B)는 P(A)P_A(B)와 같다.

3가지 사건 A, B, C가 있을 때 P_A(B), P_B(C)등과 A와 B가 일어났을 때 C의 조건부 확률 P_A∩B(C)=P(A∩B∩C)/P(A∩B)등을 정의할 수 있다.

예를 들어 항아리 속에 같은 크기를 지닌 공이 40개 들어 있다고 하자. 이중 14개는 빨간색이고 26개는 파란색이다. 또 이들 공은 무거운 것과 가벼운 것 2가지 중 1가지 재질로 되어 있으며 빨간 공은 8개가, 파란 공은 10개가 무겁다.

항아리는 암실 속에 있고 손으로 무거운 공 하나를 집어냈을 때, 이것이 빨간 공일 확률은 (빨갛고 무거울 확률)/(무거운 확률)=(8/40)/(18/40)=4/9이다.

또 밝은 곳에서 공을 만지지 않고 빨간 공을 하나 골랐을 때 이것이 무거운 공일 확률은(빨갛고 무거울 확률)/(빨간 공일 확률)=(8/40)/(14/40)=4/7이다. 이들 확률은 40개의 기본사건으로 된 확률공간에서 각각 무거운 공을 골랐거나, 빨간 공을 골랐다는 조건하에서 빨간 공이나 무거운 공이 선택되는 조건부 확률이다. 배반사건의 열 H₁, H₂, ……, H_n이 있고 그 합을 전체사건이라고 하자. 임의의 사건 A에 대해 관계식 P(A)=P(A∩H₁)＋P(A∩H₂)＋……＋P(A∩H_n)과 P(A∩H_i)=P(A)P(H_i/A)=P(H_i)P(A/H_i)를 이용해 P(A∩H_i)/P(A)를 다시 쓰면,

을 얻을 수 있다.

이것을 베이스의 정리라고 한다.

확률

조건부 확률의 특별한 경우로서 사건 A와 B가 독립인 경우 P_A(B)를 생각해보자. P(A∩B)=P(A)P(B)이므로, P_A(B)=P(B)가 되며, 마찬가지로 P_B(A)=P(A)도 성립한다.

3가지 사건 A, B, C가 독립일 때, P_A∩B(C)=P(C), P_B∩C(A)=P(A), P_C∩A(B)=P(B)가 성립한다.

또P_A(B)=P(B)이므로 P(A∩B∩C)=P(A)P(B)P(C)가 성립하며 독립성을 정의한 식과 일치한다.

여기서 다음과 같은 합사건에 대한 공식도 나온다.

P(A∪B)=P(A)＋P(B)－P(A∩B)

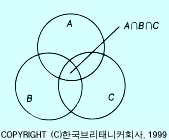
P(A∪B∪C)=P(A)＋P(B)＋P(C)－P(A∩B)－P(B∩C)－P(C∩A)＋P(A∩B∩C)

이것은 그림에서 쉽게 알 수 있다.

순열과 조합

유한개의 기본사건으로 된 경우, 사건의 확률을 구하는 문제는 순열과 조합의 수를 세는 것에 귀착되는 경우가 많다. 앞에서 든 4개의 문자를 나열하는 예에서 어느 나열방식이나 같은 정도로 일어나기 쉽다고 했기 때문에 문제의 조건에 맞는 나열방식이 몇 가지인가 하는 것은 순열의 문제가 된다.

이것은 문자 개수가 늘어도 마찬가지이며 기본적인 계산에는 서로 다른 n개에서 r개를 취해 일렬로 나열하는 방법은 모두_nP_r=n(n－1)(n－2)……(n－r＋1)=n!/(n－r)!개만큼 있다는 것을 이용한다.

1회 시행하여 성공할 확률이 p(0〈p〈1)인 베르누이 시행을 n회 반복한다고 하자. n회 중 k회 성공(따라서 n－k회 실패)할 가능성은 얼마인가? 이는 성공한 k회가 어느 시행이었는지 그 경과를 지정하는 방법의 수에 달려 있다. 그것은 n개에서 k개를 취하는 조합의 수 _nC_k=_nP_k/K!과 같다.

그리고 각각의 확률은 독립된 시행 결과이므로 p^kq^n─k이다(q=1－p). 따라서 k회 성공할 확률은 조합을 이용하면 _nC_kP^kq^n-k임을 알 수 있다.